Time and Space Complexities of Popular Algorithms
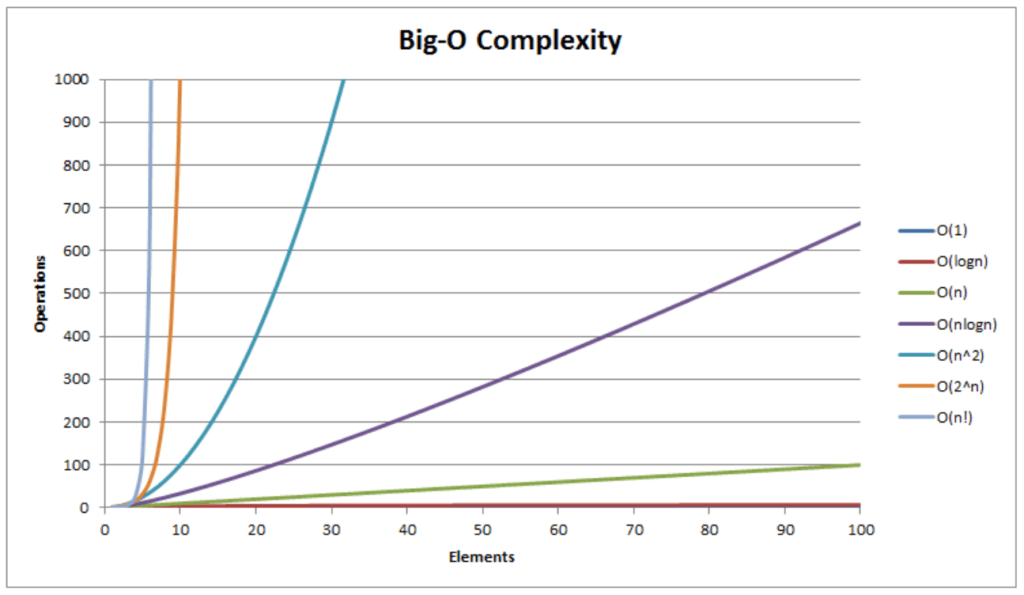
Big-O Complexity
This is the algorithm’s worst-case complexity.
Time complexity – It is defined as the number of times a particular instruction has been executed rather than the total time taken by the entire program execution.
Space Complexity – It is defined as the total memory required by a program for its execution.
Types of Time Complexities
There are 3 types of time complexities that exist.
1] Best Time – It is the minimum time taken by the algorithm. Ex. if you are performing a linear search, if the element is present at the beginning of the array.
2] Average Time – It is averaged over all possible inputs. It’s calculated by dividing the total computing time for all inputs by the total number of inputs.
3] Worst Time – It is the maximum time taken by the algorithm. Ex. if you are performing a linear search, if the element is present at the last position of the array.
Notation for Time Complexities
1] Omega notation(Ω):- This notation describes the best-case scenario of the algorithm.
2] Theta notation:- This notation describes the average-case scenario of the algorithm.
3] Big-O notation (O): – This notation describes the worst-case scenario of the algorithm.
Some common Time complexity Notations
| Notation | Meaning |
|---|---|
| O(1) | Constant Time |
| O(log n) | Logarithmic Time |
| O(n) | Linear Time |
| O(n long) | Logarithmic-linear time |
| O(n^2) | Quadratic Time |
| O(n^3) | Cubic Time |
| O(2^n) | Exponential Time |
| O(n!) | Factorial Time |
Time and Space Complexities of Sorting Algorithms
| Algorithm | Worst Space Complexity | Best Time Complexity | Average Time Complexity | Worst Time Complexity |
|---|---|---|---|---|
| Selection Sort | O(1) | Ω(n^2) | θ(n^2) | O(n^2) |
| Bubble Sort | O(1) | Ω(n) | O(n^2) | O(n^2) |
| Insertion Sort | O(1) | Ω(n) | θ(n^2) | O(n^2) |
| Heap Sort | O(1) | Ω(n log(n)) | θ(n log(n)) | O(n log(n)) |
| Quick Sort | O(n) | Ω(n log(n)) | θ(n log(n)) | O(n^2) |
| Merge Sort | o(n) | Ω(n log(n)) | θ(n log(n)) | O(n log(n)) |
| Bucket Sort | O(n) | Ω(n +k) | θ(n +k) | O(n^2) |
| Radix Sort | O(n+k) | Ω(nk) | θ(nk) | O(nk) |
| Count Sort | O(k) | Ω(n +k) | θ(n +k) | O(n +k) |
| Shell Sort | O(1) | Ω(n log(n)) | θ(n log(n)) | O(n^2) |
| Tim Sort | O(n) | Ω(n) | θ(n log(n)) | O(n log (n)) |
| Tree Sort | O(n) | Ω(n log(n)) | θ(n log(n)) | O(n^2) |
| Cube Sort | O(n) | Ω(n) | θ(n log(n)) | O(n log(n)) |
Time and Space Complexities of Searching Algorithms
| Algorithm | Worst Space Complexity | Best Time Complexity | Avarage Time Complexity | Worst Time Complexity |
|---|---|---|---|---|
| Linear Search | O(1) | O(1) | O(n) | O(n) |
| Binary Search | O(1) | O(1) | O(log n) | O(log n) |
| Jump Search | O(1) | O(√n) | O(√n) | O(n) |
| Interpolation Search | O(1) | O(log n) | O(log n) | O(n) |
| Fibonacci Search | O(1) | O(log n) | O(log n) | O(n) |
Download Link – Click Here






