Design and Analysis of Algorithm Lab 4 | Read Now

Design and Analysis of Algorithm Lab 4

4] Sort a given set of n integer elements using the quick sort method and compute its time complexity. Run the program for varied values of n>5000 and record the time taken to sort. Plot a graph of the time taken versus nongraph sheet. The elements can be read from a file or can be generated using the random number generator. Demonstrate using Java how the divide and conquer method works along with its time complexity analysis: worst case, average case, and best case.

4] Program code

import java.util.Random;
import java.util.Scanner;
public class lab4
{
	public static void main(String[] args) 
	{
		int a[]= new int[100000];
		Scanner in = new Scanner(System.in);
		long start, end;

		System.out.println("QUICK SORT PROGRAM");
		System.out.println("Enter the number of elements to be sorted");		
		int n = in.nextInt();
		Random rand= new Random();
		for(int i=0;i<n;i++)
			a[i]=rand.nextInt(100);

		System.out.println("Array elements to be sorted are");
		for(int i=0; i<n; i++)
			System.out.print(a[i]+" ");
		a[n]=999;
		start=System.nanoTime();
		quicksort(a,0,n-1);
		end=System.nanoTime();
	
		System.out.println("\nThe sorted elements are");
		for(int i=0; i<n; i++)
			System.out.print(a[i]+" ");
	
		System.out.println("\nThe time taken to sort is "+(end-start)+"ns");
	}
	
	static void quicksort(int a[],int p, int q)
	{
		int j;
		if(p < q)
		{
			j=partition(a,p,q);
			quicksort(a,p,j-1);
			quicksort(a,j+1,q);
		}
	}

	static int partition(int a[],int m, int p)
	{
		int v, i, j;
		v=a[m]; // first element is pivot element
		i=m;
		j=p;
		while(i <= j)
		{
			while(a[i] <= v)
			i++;
			while(a[j] > v)
			j--;
			if(i < j)
				interchange(a,i,j);
		}
		a[m] = a[j];
		a[j] = v;
		return j;
	}
	
	static void interchange(int a[], int i, int j)
	{
		int p;
		p = a[i];
		a[i] = a[j];
		a[j] = p;
	}
}

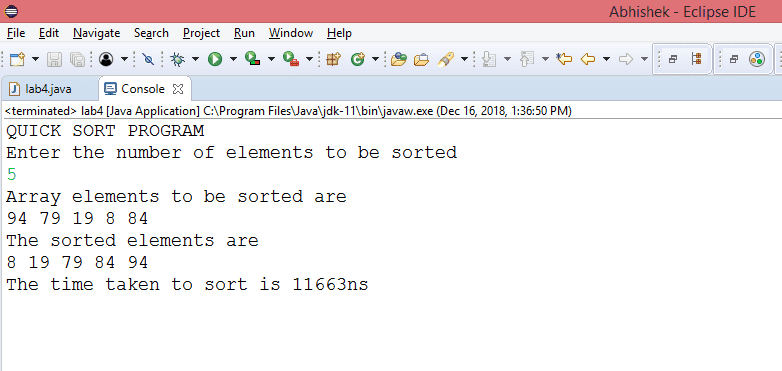
Output